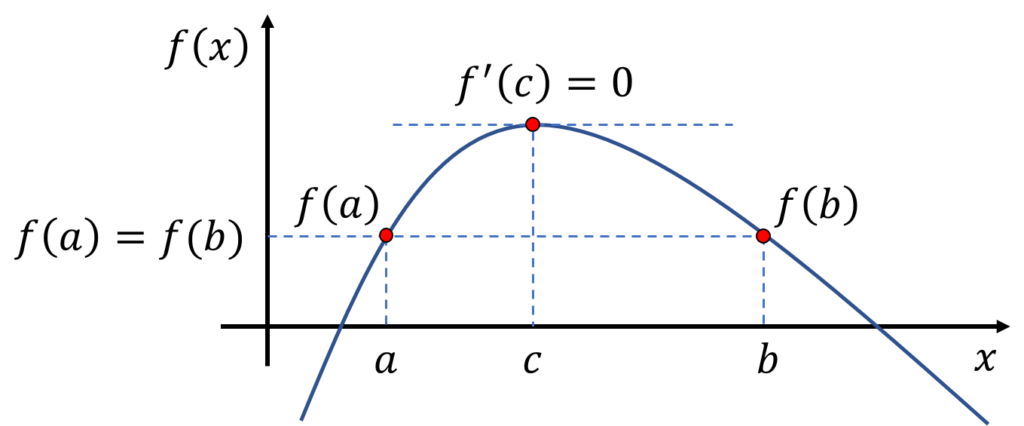
ロルの定理

ロルの定理とは，微分可能な関数で，

$$f(a)=f(b),~~(a \neq b)$$

となるような\(a\)，\(b\)があるとき，

$$f'(c)=0$$

となる\(c\)が区間\([a,b]\)内に1つは存在するという定理である．

証明

区間\([a,b]\)における以下の3つの場合分けをして考える．

\begin{align*}
&(1)~ f(x)=\rm{const}\\
&(2)~ f(a)=f(b)\leq f(t)\\
&(3)~ f(a)=f(b)\geq f(t)
\end{align*}

(1)は，任意の\(c\)で\(f'(c)=0\)となる．

(2)は，(2)式を満たす\(t\)が存在するときに，最大値・最小値の定理より，最大値となるような\(c\)が存在する．\(f(x)\)は\(c\)点で微分可能であり，

$$f(c)\geq f(c+\Delta x)$$

であることを考慮すれば，

\begin{align*}
f'(c)=\lim_{\Delta x\to +0} \frac{f(c+\Delta x)-f(c)}{\Delta x}\leq 0\\
f'(c)=\lim_{\Delta x\to -0} \frac{f(c+\Delta x)-f(c)}{\Delta x}\geq 0
\end{align*}

よって，\(f'(c)=0\)となる．

(3)は，(3)式を満たす\(t\)が存在するときに，最大値・最小値の定理より最小値となるような\(c\)が存在する．これも(2)と同様に考えると\(f'(c)=0\)を得る．

よって，ロルの定理が証明された．