平均値定理

2022年05月06日数学系, 解析学, 解析学諸定理

ラグランジュの平均値定理

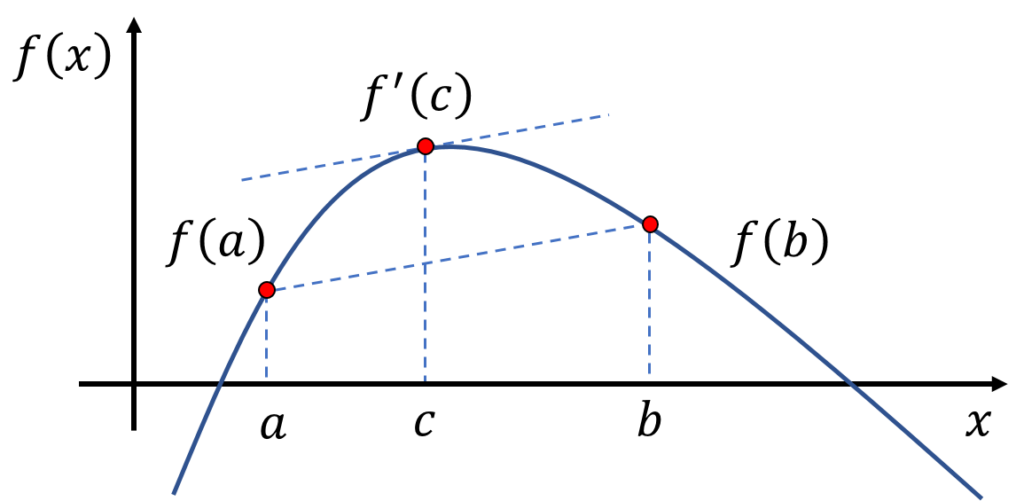
ラグランジュの平均値定理とは，ある区間$[a,b]$において，$a,b$での微分可能であるとき，$a,b$を結んだ直線の傾きと同じ傾きをもつ点$c$が区間$[a,b]$内に存在するという定理である．

$$\frac{f(b)-f(a)}{b-a}=f'(c)$$
$$a\leq c\leq b$$

関数$g(x)$を以下のように「関数$f(x)$」+「$Ax$」で与える．

$$g(x)=f(x)+Ax$$

ここで，$g(a)=g(b)$となるような$A$について求めると，

\begin{align*}
f(a)+Aa&=f(b)+Ab\\
\therefore A&=-\frac{f(b)-f(a)}{b-a}
\end{align*}

求めた$A$を$g(x)$に代入すれば，$g(a)=g(b)$となるので，ロルの定理を適用して，$g'(c)=0$となる$c$が存在することから，

$$g'(c)=f'(c)-\frac{f(b)-f(a)}{b-a}$$

以上より，ラグランジュの平均値定理が示された．

コーシーの平均値定理とは，ラグランジュの平均値定理を一般化したものである．

$$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(c)}{g'(c)}$$
$$a\leq c \leq b$$

関数$z(x)$を以下のように定義する．

$$z(x)=f(x)+Ag(x)$$

ここで，$z(a)=z(b)$となるような$A$について求めると，

\begin{align*}
f(a)+Ag(a)&=f(b)+Ag(b)\\
\therefore A &=-\frac{f(b)-f(a)}{g(b)-g(a)}
\end{align*}

求めた$A$を$z(x)$に代入すれば，$z(a)=z(b)$となるので，ロルの定理を適用して，$z'(c)=0$となる$c$が存在することから，

$$z'(c)=f'(c)-\frac{f(b)-f(a)}{g(b)-g(a)}g'(c)=0$$

以上より，コーシーの平均値定理が示された．