単振動

単振動とは，ある1つの物体がばね（変位に比例した力の要素：復元力）によって振動する現象のことをいう．

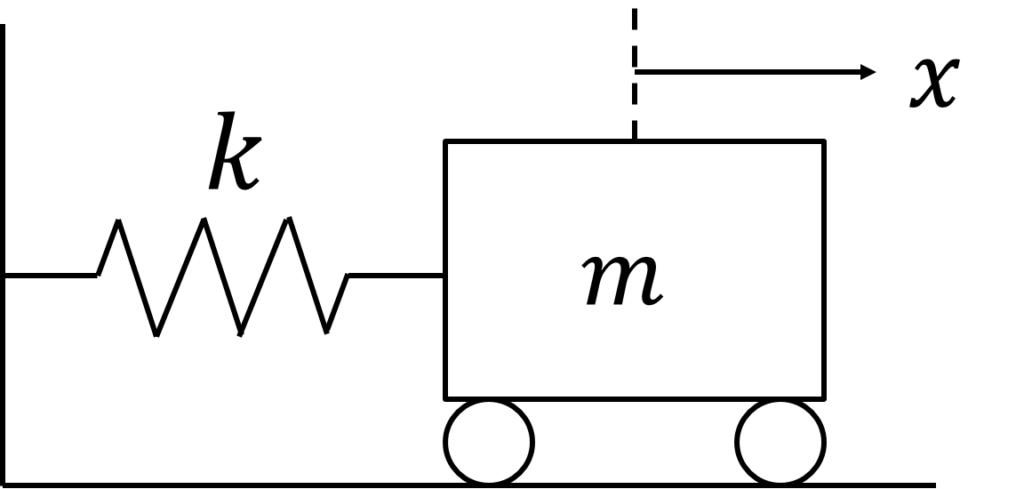
ニュートンの運動の法則とフックの法則から上図の運動方程式は以下のように表される．

$$\frac{d^2 x(t)}{dt^2}=-kx(t)$$

上式の運動方程式の特性方程式の解は以下のようになる．

\begin{align*}
m\lambda^2&=-k\\
\therefore\lambda&=\pm j\sqrt{\frac{k}{m}}
\end{align*}

よって，特性方程式の解が虚数解であるから，単振動の運動方程式の解は以下のようになる．

$$x(t)=C\cos{\sqrt\frac{k}{m}t}+S\sin{\sqrt\frac{k}{m}t}$$

ここで，\(C\)と\(S\)は初期変位，初期速度から決定されるパラメータである．これを，三角関数の合成すれば，

\begin{align*}
x(t)&=A\cos(\omega t+\varphi)\\
A&=\sqrt{C^2+S^2}\\
\varphi&=\tan^{-1}{\frac{S}{C}}\\
\omega&=\sqrt\frac{k}{m}
\end{align*}

上式から，変位\(x(t)\)は角振動数\(\omega\)の周期関数であることがわかる．ここで，\(A\)を「振幅」といい，\(\omega\)を「（不減衰）固有角振動数」，\(\varphi\)を「初期位相」という．