運動方程式
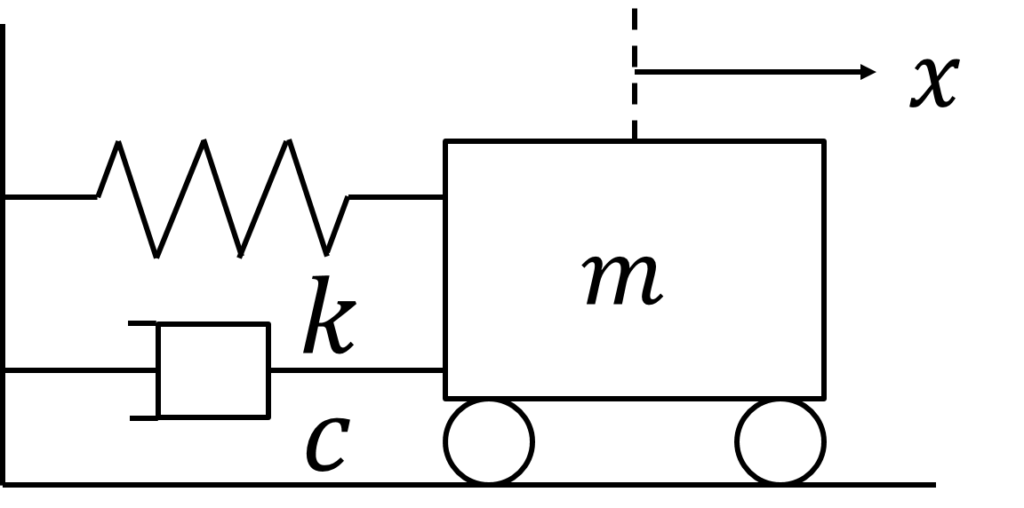
上図のような質量\(m\)の物体および粘性係数\(c\)のダンパ,ばね定数\(k\)のばねによる運動系がある場合,この運動系の運動方程式は以下のようになる.
$$m\ddot{x}+c\dot{x}+kx=0$$
運動の様子
運動方程式(EOM)の特性方程式から運動の様子を観察する.運動方程式の特性方程式は,
$$m\lambda^2+c\lambda+k=0$$
であるから,二次方程式の判別式より以下の表を得る.ただし,\(C, S\)は初期条件等から決定される任意定数である.
| 判別式 | 特性方程式の解 | 一般解 | |
| 1 | $$c^2-4mk>0$$ | $$\lambda_{1,2}=\frac{-c\pm\sqrt{c^2-4mk}}{2m}$$ | $$x(t)=Ce^{\lambda_1t}+Se^{\lambda_2t}$$ |
| 2 | $$c^2-4mk=0$$ | $$\lambda=\frac{-c}{2m}$$ | $$x(t)=Ce^{\lambda t}+Ste^{\lambda t}$$ |
| 3 | $$c^2-4mk<0$$ | \begin{align*} \lambda_{1,2}&=\alpha+j\beta\\ &=\frac{-c}{2m}\pm j\frac{\sqrt{4mk-c^2}}{2m} \end{align*} | $$x(t)=e^\alpha(C\cos{\beta t}+S\sin{\beta t})$$ |
上表において,
1の状態になることを「過減衰」
2の状態になることを「臨界減衰」
3の状態になることを「不足減衰」
という.
上表をもとに1~3の結果をグラフに描くと以下のようになる.
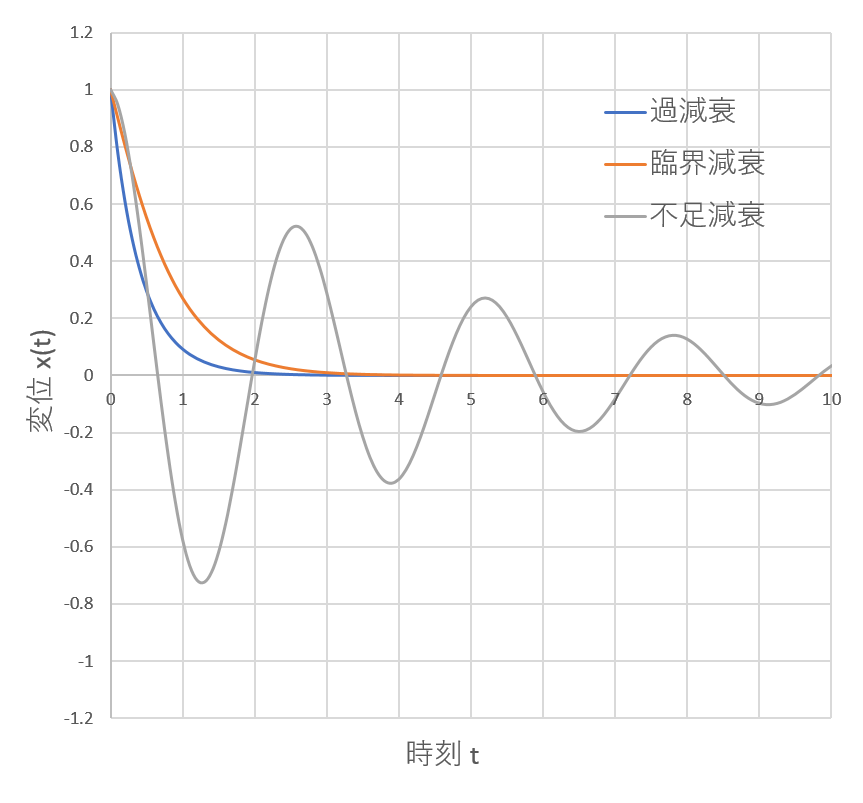
上式のことから,1,2の運動は振動しないで収束していくが,3の運動は振動しながら収束していくことがわかる.
臨界減衰係数・減衰比
「臨界減衰係数」臨界減衰となる粘性係数のパラメータのことである.
$$c_c=2\sqrt{mk}$$
「減衰比」とは,臨界減衰係数と粘性係数の比率のことである.
$$\zeta=\frac{c}{c_c}=\frac{c}{2\sqrt{mk}}$$
固有角振動数
「固有角振動数」とは,振動解において振動の様子を表すパラメータである.減衰を考慮しない(\(c=0\))固有角振動数のことを「不減衰固有角振動数」(\(\omega_n\))といい,減衰を考慮する(\(c\neq0\))固有角振動数を「減衰固有角振動数」(\(\omega_d\))といい,以下のように表される.
\begin{align*}
\omega_n &= \sqrt{\frac{k}{m}}\\
\omega_d &=\sqrt{\frac{4mk-c^2}{4m^2}}=\omega_n\sqrt{1-\zeta^2}
\end{align*}